Estimation of tree height using GEDI dataset - Random Forest prediction

In order to run this notebook, please do what follows:

cd  /media/sf_LVM_shared/my_SE_data/exercise
source $HOME/venv/bin/activate
pip3 install pyspatialml
jupyter lab Tree_Height_03RF_pred
Find a relationship between tree height and enviromental predictors to be able to predict out side the GEDI observation.
The model, in its simplest form, looks like the following:
y ~ f ( a*x1 + b*x2 + c*x3 + …)  + ε,

where y is a response variable, the x’s are predictor variables, and ε is the associated error.

There are many different types of models

  • Parametric models – make assumptions about the underlying distribution of the data.

    • Maximum likelihood classification

    • Discriminant analysis

    • General linear models (ex. linear regression)

  • Nonparametric models – make no assumptions about the underlying data distributions.

    • Generalized additive models

    • Support Vector Machine

    • Artificial neural networks

    • Random Forest

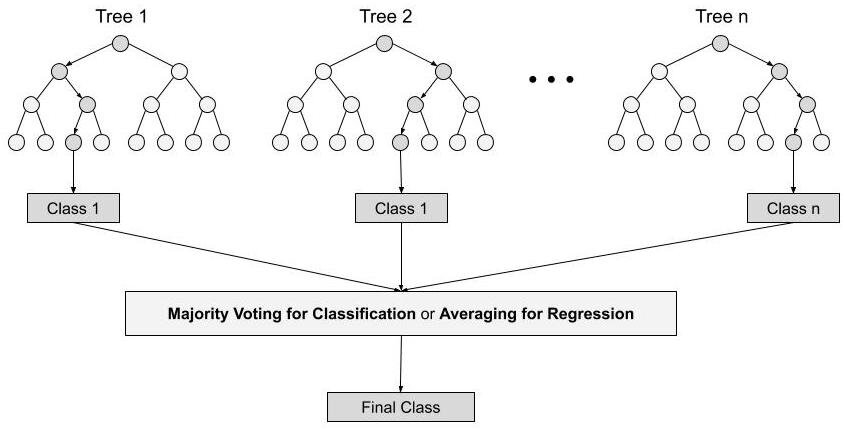
Random forest

Random forest is a Supervised Machine Learning Algorithm that is used widely in Classification (containing categorical variables) and Regression (response continuous variables) problems. It builds decision trees on different samples and takes their majority vote for classification and average in case of regression.

One of the most important features of the Random Forest Algorithm is that it can handle continuous and categorical variables predictors without any assamption on their data distribution, dimension, and even if the predictors are autocorrelated.

Bagging
Bagging, also known as Bootstrap Aggregation is the ensemble technique used by random forest. Choosesing a random sample from the data set it is creating a tree. Each tree is generated from the samples (Bootstrap Samples) provided by the Original Data with replacement known as row sampling. This step of row sampling with replacement is called bootstrap. Each is trained independently which generates results. The final output is based on majority voting after combining the results of all models. This step which involves combining all the results and generating output based on majority voting is known as tree aggregation.

Steps involved in random forest algorithm:

  • Step 1: In Random forest n number of random records are taken from the data set having k number of records.

  • Step 2: Individual decision trees are constructed for each sample.

  • Step 3: Each decision tree will generate an output.

  • Step 4: Final output is considered based on Majority Voting or Averaging for Classification and regression respectively.

(source https://www.analyticsvidhya.com/blog/2021/06/understanding-random-forest/)

[2]:

from IPython.display import Image
Image("../images/Random_Forest.jpg" , width = 700, height = 700)

[2]:
../_images/CASESTUDY_Tree_Height_03RF_pred_5_0.jpg
Random Forest exercise
In this exercise we will use Random Forest Regression algorithm with the sklearn python package to estimage the tree height. In last step, we are going to use the Pyspatialml for the spatial prediction on the raster files.
[7]:

import pandas as pd
import numpy as np
import rasterio
from rasterio import *
from rasterio.plot import show
# from pyspatialml import Raster
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.pipeline import Pipeline
from scipy.stats import pearsonr
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (10,6.5)

Import raw data, extracted predictors and show the data distribution

[4]:

predictors = pd.read_csv("tree_height/txt/eu_x_y_height_predictors_select.txt", sep=" ",  index_col=False)
pd.set_option('display.max_columns',None)
# change column name
predictors = predictors.rename({'dev-magnitude':'devmagnitude'} , axis='columns')
predictors.head(10)

[4]:
ID X Y h BLDFIE_WeigAver CECSOL_WeigAver CHELSA_bio18 CHELSA_bio4 convergence cti devmagnitude eastness elev forestheight glad_ard_SVVI_max glad_ard_SVVI_med glad_ard_SVVI_min northness ORCDRC_WeigAver outlet_dist_dw_basin SBIO3_Isothermality_5_15cm SBIO4_Temperature_Seasonality_5_15cm treecover
0 1 6.050001 49.727499 3139.00 1540 13 2113 5893 -10.486560 -238043120 1.158417 0.069094 353.983124 23 276.871094 46.444092 347.665405 0.042500 9 780403 19.798992 440.672211 85
1 2 6.050002 49.922155 1454.75 1491 12 1993 5912 33.274361 -208915344 -1.755341 0.269112 267.511688 19 -49.526367 19.552734 -130.541748 0.182780 16 772777 20.889412 457.756195 85
2 3 6.050002 48.602377 853.50 1521 17 2124 5983 0.045293 -137479792 1.908780 -0.016055 389.751160 21 93.257324 50.743652 384.522461 0.036253 14 898820 20.695877 481.879700 62
3 4 6.050009 48.151979 3141.00 1526 16 2569 6130 -33.654274 -267223072 0.965787 0.067767 380.207703 27 542.401367 202.264160 386.156738 0.005139 15 831824 19.375000 479.410278 85
4 5 6.050010 49.588410 2065.25 1547 14 2108 5923 27.493824 -107809368 -0.162624 0.014065 308.042786 25 136.048340 146.835205 198.127441 0.028847 17 796962 18.777500 457.880066 85
5 6 6.050014 48.608456 1246.50 1515 19 2124 6010 -1.602039 17384282 1.447979 -0.018912 364.527100 18 221.339844 247.387207 480.387939 0.042747 14 897945 19.398880 474.331329 62
6 7 6.050016 48.571401 2938.75 1520 19 2169 6147 27.856503 -66516432 -1.073956 0.002280 254.679596 19 125.250488 87.865234 160.696777 0.037254 11 908426 20.170450 476.414520 96
7 8 6.050019 49.921613 3294.75 1490 12 1995 5912 22.102139 -297770784 -1.402633 0.309765 294.927765 26 -86.729492 -145.584229 -190.062988 0.222435 15 772784 20.855963 457.195404 86
8 9 6.050020 48.822645 1623.50 1554 18 1973 6138 18.496584 -25336536 -0.800016 0.010370 240.493759 22 -51.470703 -245.886719 172.074707 0.004428 8 839132 21.812290 496.231110 64
9 10 6.050024 49.847522 1400.00 1521 15 2187 5886 -5.660453 -278652608 1.477951 -0.068720 376.671143 12 277.297363 273.141846 -138.895996 0.098817 13 768873 21.137711 466.976685 70 
[5]:

len(predictors)

[5]:

1267239

Plotting the data

[6]:

bins = np.linspace(min(predictors['h']),max(predictors['h']),100)
plt.hist((predictors['h']),bins,alpha=0.8);
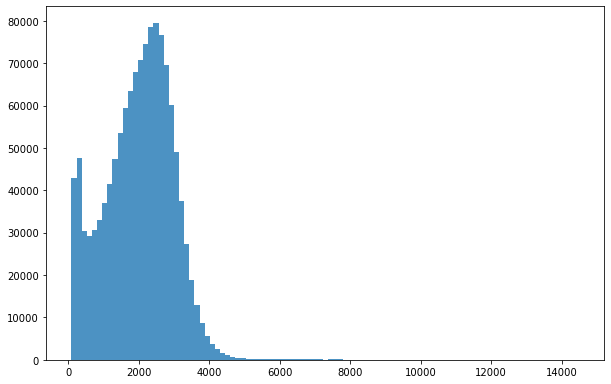
../_images/CASESTUDY_Tree_Height_03RF_pred_12_0.png

Select only tree with height less then 70m (highest tree in germany 67m https://visit.freiburg.de/en/attractions/waldtraut-germany-s-tallest-tree)

[7]:

predictors_sel = predictors.loc[(predictors['h'] < 7000)  ].sample(100000)
predictors_sel.insert ( 4, 'hm' ,  predictors_sel['h']/100 ) # add a culumn of heigh in meter
len(predictors_sel)
predictors_sel.head(10)

[7]:
ID X Y h hm BLDFIE_WeigAver CECSOL_WeigAver CHELSA_bio18 CHELSA_bio4 convergence cti devmagnitude eastness elev forestheight glad_ard_SVVI_max glad_ard_SVVI_med glad_ard_SVVI_min northness ORCDRC_WeigAver outlet_dist_dw_basin SBIO3_Isothermality_5_15cm SBIO4_Temperature_Seasonality_5_15cm treecover
211869 211870 6.763981 49.923656 2504.00 25.0400 1533 13 2114 6069 -51.807003 -204555312 1.713994 -0.030101 356.479462 23 168.107666 0.701416 -27.481689 0.001850 15 667874 19.075720 444.208923 95
1243664 1243665 9.833275 49.526917 649.25 6.4925 1534 15 2102 6516 0.582322 -200281328 -0.082161 0.021150 338.562622 23 663.329102 66.410156 208.560791 -0.054791 8 801897 18.012062 487.378571 89
862800 862801 8.747207 49.396667 4145.25 41.4525 1464 13 2770 6187 -5.705454 -193031872 2.207440 0.082736 471.601471 29 682.764160 196.173340 410.016113 -0.105913 9 687733 19.400467 449.129852 85
184466 184467 6.692364 48.311297 902.75 9.0275 1503 16 2458 6333 2.532082 -153840256 -0.687262 -0.040297 326.341187 12 -155.665771 -179.105957 -273.086426 0.005218 11 938821 19.768513 504.342621 86
210193 210194 6.759972 48.427197 1215.75 12.1575 1499 11 2473 6283 -34.008671 -184876336 0.869934 0.029229 331.943359 26 214.386475 39.022705 -19.717529 -0.010323 20 937918 18.850109 450.874207 45
485841 485842 7.421320 48.972783 2629.50 26.2950 1443 13 2366 6249 -12.187319 -237638256 0.527734 0.184359 317.114014 25 55.184082 58.465332 91.532715 -0.045335 10 828316 19.876814 445.643494 73
120379 120380 6.482271 49.914016 2173.00 21.7300 1538 16 1847 6105 -17.632570 -197189520 -1.088760 -0.035505 272.008911 23 -126.860352 -195.746094 75.838867 -0.008322 18 728450 19.971024 459.339722 97
388316 388317 7.193769 48.376309 527.00 5.2700 1460 11 2972 6227 24.105930 -287456672 -1.292012 0.108061 523.706970 11 309.591309 440.787842 600.310059 0.088250 17 870673 20.666460 459.003754 11
825800 825801 8.663616 49.674021 2836.25 28.3625 1533 14 2789 6461 19.265608 -253300688 -0.924922 -0.056384 208.336411 26 155.725586 211.511230 500.423096 0.082024 10 649353 20.394165 502.623260 85
1116257 1116258 9.384341 49.143288 1670.00 16.7000 1527 14 2207 6644 8.773687 -330216832 -0.236958 -0.159152 255.992538 26 154.274658 110.248535 181.868408 0.074600 5 780885 19.781750 518.130005 72

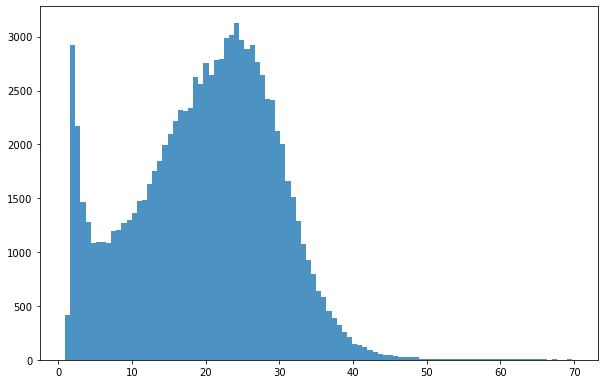
Plotting response variables distribution

[8]:

bins = np.linspace(min(predictors_sel['hm']),max(predictors_sel['hm']),100)
plt.hist((predictors_sel['hm']),bins,alpha=0.8);
../_images/CASESTUDY_Tree_Height_03RF_pred_16_0.png

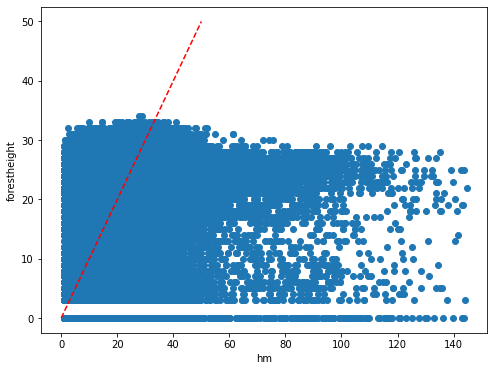
The Global Forest Canopy Height, 2019 map has been release in 2020 (scientific publication https://doi.org/10.1016/j.rse.2020.112165). The authors use a regression tree model that was calibrated and applied to each individual Landsat GLAD ARD tile (1 × 1◦) in a “moving window” mode. Such tree height estimation is storede in forestheight.tiff and in the table as forestheight column. A correlation plot and its pearson coefficient is show below.

[9]:

plt.rcParams["figure.figsize"] = (8,6)
plt.scatter(predictors['h']/100,predictors['forestheight'])
plt.xlabel('hm')
plt.ylabel('forestheight')
ident = [0, 50]
plt.plot(ident,ident,'r--')


[9]:

[<matplotlib.lines.Line2D at 0x7fa02257ddb0>]
../_images/CASESTUDY_Tree_Height_03RF_pred_18_1.png 
[10]:

pearsonr_Publication_Estimation = pearsonr(predictors['h'],predictors['forestheight'])[0]
pearsonr_Publication_Estimation

[10]:

0.4527925129990046

We will try to beats such error estimation using a more advance ML tecnques and different enviromental predictors that better express the ecological condition.

Data set splitting

Split the dataset (predictors_sel) in order to create response variable vs predictors variables (we are excluding forestheight predictors).

[11]:

   X = predictors_sel.iloc[:,[5,6,7,8,9,10,11,12,13,15,16,17,18,19,20,21,22,23]].values
Y = predictors_sel.iloc[:,4:5].values
feat = predictors_sel.iloc[:,[5,6,7,8,9,10,11,12,13,15,16,17,18,19,20,21,22,23]].columns.values

Double ceck that we select the right columns

[12]:

feat

[12]:

array(['BLDFIE_WeigAver', 'CECSOL_WeigAver', 'CHELSA_bio18',
       'CHELSA_bio4', 'convergence', 'cti', 'devmagnitude', 'eastness',
       'elev', 'glad_ard_SVVI_max', 'glad_ard_SVVI_med',
       'glad_ard_SVVI_min', 'northness', 'ORCDRC_WeigAver',
       'outlet_dist_dw_basin', 'SBIO3_Isothermality_5_15cm',
       'SBIO4_Temperature_Seasonality_5_15cm', 'treecover'], dtype=object)

[13]:

Y.shape

[13]:

(100000, 1)

[14]:

X.shape

[14]:

(100000, 18)

Create 4 dataset for training and testing the algorithm

[15]:

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5, random_state=24)
y_train = np.ravel(Y_train)
y_test = np.ravel(Y_test)

Random Forest default parameters

Random Forest can be implemented using the RandomForestRegressor in scikit-learn

Training Random Forest using default parameters

[16]:

rf = RandomForestRegressor(random_state = 42)
rf.get_params()

[16]:

{'bootstrap': True,
 'ccp_alpha': 0.0,
 'criterion': 'mse',
 'max_depth': None,
 'max_features': 'auto',
 'max_leaf_nodes': None,
 'max_samples': None,
 'min_impurity_decrease': 0.0,
 'min_impurity_split': None,
 'min_samples_leaf': 1,
 'min_samples_split': 2,
 'min_weight_fraction_leaf': 0.0,
 'n_estimators': 100,
 'n_jobs': None,
 'oob_score': False,
 'random_state': 42,
 'verbose': 0,
 'warm_start': False}

[17]:

rfReg = RandomForestRegressor(min_samples_leaf=50, oob_score=True)
rfReg.fit(X_train, y_train);
dic_pred = {}
dic_pred['train'] = rfReg.predict(X_train)
dic_pred['test'] = rfReg.predict(X_test)
pearsonr_all = [pearsonr(dic_pred['train'],y_train)[0],pearsonr(dic_pred['test'],y_test)[0]]
pearsonr_all

[17]:

[0.6043347073198263, 0.5189400044676861]

[18]:

# checking the oob score
rfReg.oob_score_

[18]:

0.2651550005190103
Additional resources how to reduce the oob error can found at
https://scikit-learn.org/stable/auto_examples/ensemble/plot_ensemble_oob.html

Random Forest tuning

  • “max_features”: number of features to consider when looking for the best split.

  • “max_samples”: number of samples to draw from X to train each base estimator.

  • “n_estimators”: identify the number of trees that must grow. It must be large enough so that the error is stabilized. Defoult 100.

  • “max_depth”: max number of levels in each decision tree.

Using this pseudo code tune the parameters in order the improve the algoirithm performance

pipeline = Pipeline([('rf',RandomForestRegressor())])

parameters = {
        'rf__max_features':(3,4,5),
        'rf__max_samples':(0.5,0.6,0.7),
        'rf__n_estimators':(500,1000),
        'rf__max_depth':(50,100,200,300)}

grid_search = GridSearchCV(pipeline,parameters,n_jobs=6,cv=5,scoring='r2',verbose=1)
grid_search.fit(X_train,y_train)


rfReg = RandomForestRegressor(n_estimators=5000,max_features=0.33,max_depth=500,max_samples=0.7,n_jobs=-1,random_state=24 , oob_score = True)
rfReg.fit(X_train, y_train);
dic_pred = {}
dic_pred['train'] = rfReg.predict(X_train)
dic_pred['test'] = rfReg.predict(X_test)
pearsonr_all_tune = [pearsonr(dic_pred['train'],y_train)[0],pearsonr(dic_pred['test'],y_test)[0]]
pearsonr_all_tune

grid_search.best_score_

print ('Best Training score: %0.3f' % grid_search.best_score_)
print ('Optimal parameters:') best_par = grid_search.best_estimator_.get_params()
for par_name in sorted(parameters.keys()):
    print ('\t%s: %r' % (par_name, best_par[par_name]))

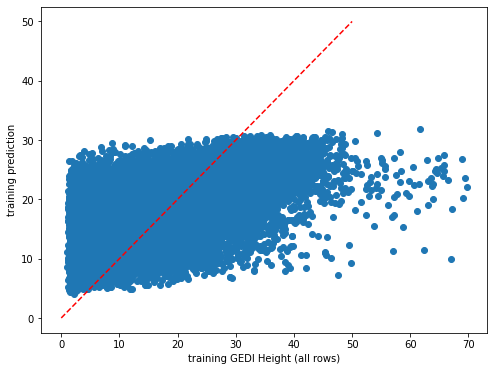
Tracking the error rate trend as in https://scikit-learn.org/stable/auto_examples/ensemble/plot_ensemble_oob.html

[19]:

plt.rcParams["figure.figsize"] = (8,6)
plt.scatter(y_train,dic_pred['train'])
plt.xlabel('training GEDI Height (all rows)')
plt.ylabel('training prediction')
ident = [0, 50]
plt.plot(ident,ident,'r--')

[19]:

[<matplotlib.lines.Line2D at 0x7fa02261eec0>]
../_images/CASESTUDY_Tree_Height_03RF_pred_36_1.png 
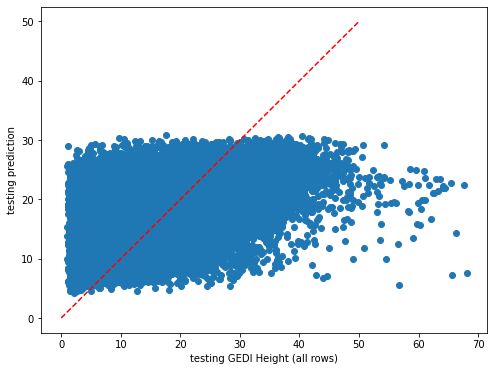
[20]:

plt.rcParams["figure.figsize"] = (8,6)
plt.scatter(y_test,dic_pred['test'])
plt.xlabel('testing GEDI Height (all rows)')
plt.ylabel('testing prediction')
ident = [0, 50]
plt.plot(ident,ident,'r--')

[20]:

[<matplotlib.lines.Line2D at 0x7fa03153b3a0>]
../_images/CASESTUDY_Tree_Height_03RF_pred_37_1.png 
[21]:

impt = [rfReg.feature_importances_, np.std([tree.feature_importances_ for tree in rfReg.estimators_],axis=1)]
ind = np.argsort(impt[0])

[22]:

ind

[22]:

array([ 1, 13,  0,  4,  6,  8, 16,  2,  5, 15, 12,  3, 11,  7,  9, 14, 10,
       17])

[23]:

plt.rcParams["figure.figsize"] = (6,12)
plt.barh(range(len(feat)),impt[0][ind],color="b", xerr=impt[1][ind], align="center")
plt.yticks(range(len(feat)),feat[ind]);
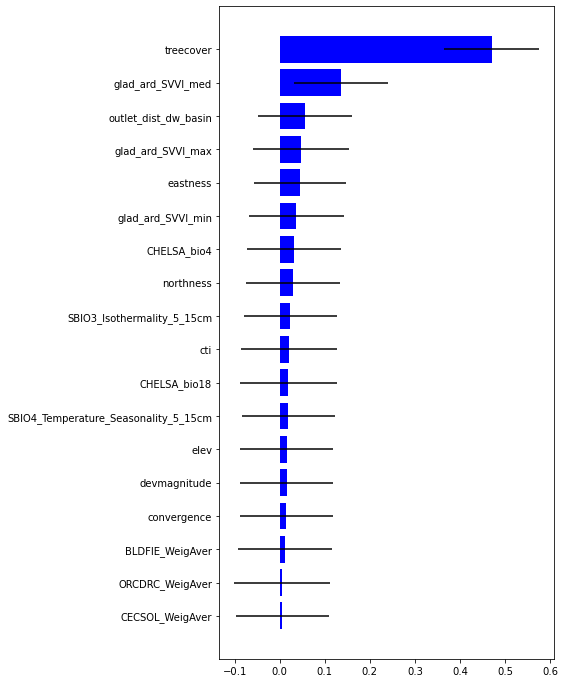
../_images/CASESTUDY_Tree_Height_03RF_pred_40_0.png

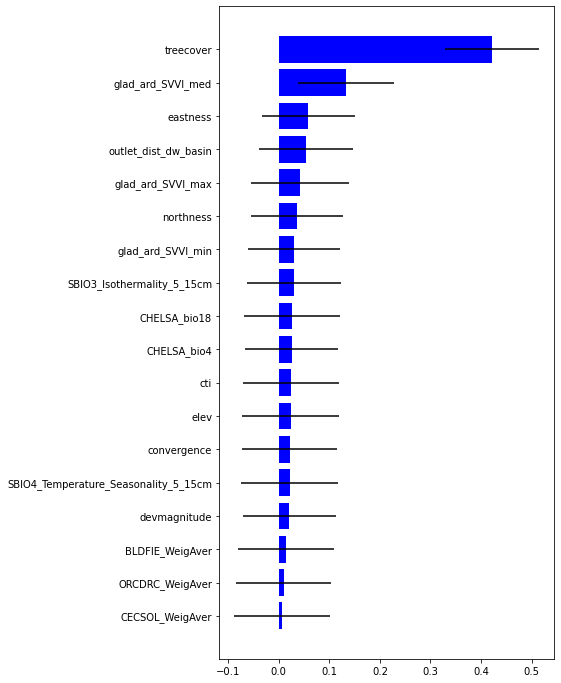
Most important variable is treecover followed by Spectral Variability Vegetation Index, followed by outlet_dist_dw_basin that is a proxy of water accumulation. Besides eastness and northness describes microclimat condition.

Base on data quality flag select more reilable tree height.

File storing tree hight (cm) obtained by 6 algorithms, with their associate quality flags. The quality flags can be used to refine and select the best tree height estimation and use it as tree height observation.

  • a?_95: tree hight (cm) at 95 quintile, for each algorithm

  • min_rh_95: minimum value of tree hight (cm) ammong the 6 algorithms

  • max_rh_95: maximum value of tree hight (cm) ammong the 6 algorithms

  • BEAM: 1-4 coverage beam = lower power (worse) ; 5-8 power beam = higher power (better)

  • digital_elev: digital mdoel elevation

  • elev_low: elevation of center of lowest mode

  • qc_a?: quality_flag for six algorithms quality_flag = 1 (better); = 0 (worse)

  • se_a?: sensitivity for six algorithms sensitivity < 0.95 (worse); sensitivity > 0.95 (beter )

  • deg_fg: (degrade_flag) not-degraded 0 (better) ; degraded > 0 (worse)

  • solar_ele: solar elevation. > 0 day (worse); < 0 night (better)

[24]:

height_6algorithms = pd.read_csv("tree_height/txt/eu_y_x_select_6algorithms_fullTable.txt", sep=" ",  index_col=False)
pd.set_option('display.max_columns',None)
height_6algorithms.head(6)

[24]:
ID X Y a1_95 a2_95 a3_95 a4_95 a5_95 a6_95 min_rh_95 max_rh_95 BEAM digital_elev elev_low qc_a1 qc_a2 qc_a3 qc_a4 qc_a5 qc_a6 se_a1 se_a2 se_a3 se_a4 se_a5 se_a6 deg_fg solar_ele
0 1 6.050001 49.727499 3139 3139 3139 3120 3139 3139 3120 3139 5 410.0 383.72153 1 1 1 1 1 1 0.962 0.984 0.968 0.962 0.989 0.979 0 17.7
1 2 6.050002 49.922155 1022 2303 970 872 5596 1524 872 5596 5 290.0 2374.14110 0 0 0 0 0 0 0.948 0.990 0.960 0.948 0.994 0.980 0 43.7
2 3 6.050002 48.602377 380 1336 332 362 1336 1340 332 1340 4 440.0 435.97781 1 1 1 1 1 1 0.947 0.975 0.956 0.947 0.981 0.968 0 0.2
3 4 6.050009 48.151979 3153 3142 3142 3127 3138 3142 3127 3153 2 450.0 422.00537 1 1 1 1 1 1 0.930 0.970 0.943 0.930 0.978 0.962 0 -14.2
4 5 6.050010 49.588410 666 4221 651 33 5611 2723 33 5611 8 370.0 2413.74830 0 0 0 0 0 0 0.941 0.983 0.946 0.941 0.992 0.969 0 22.1
5 6 6.050014 48.608456 787 1179 1187 761 1833 1833 761 1833 3 420.0 415.51581 1 1 1 1 1 1 0.952 0.979 0.961 0.952 0.986 0.975 0 0.2 
[25]:

height_6algorithms_sel = height_6algorithms.loc[(height_6algorithms['BEAM'] > 4)
                                            &   (height_6algorithms['qc_a1'] == 1)
                                            &   (height_6algorithms['qc_a2'] == 1)
                                            &   (height_6algorithms['qc_a3'] == 1)
                                            &   (height_6algorithms['qc_a4'] == 1)
                                            &   (height_6algorithms['qc_a5'] == 1)
                                            &   (height_6algorithms['qc_a6'] == 1)
                                            &   (height_6algorithms['se_a1'] > 0.95)
                                            &   (height_6algorithms['se_a2'] > 0.95)
                                            &   (height_6algorithms['se_a3'] > 0.95)
                                            &   (height_6algorithms['se_a4'] > 0.95)
                                            &   (height_6algorithms['se_a5'] > 0.95)
                                            &   (height_6algorithms['se_a6'] > 0.95)
                                            &   (height_6algorithms['deg_fg'] == 0)
                                            &   (height_6algorithms['solar_ele'] < 0)]

[26]:

height_6algorithms_sel

[26]:
ID X Y a1_95 a2_95 a3_95 a4_95 a5_95 a6_95 min_rh_95 max_rh_95 BEAM digital_elev elev_low qc_a1 qc_a2 qc_a3 qc_a4 qc_a5 qc_a6 se_a1 se_a2 se_a3 se_a4 se_a5 se_a6 deg_fg solar_ele
7 8 6.050019 49.921613 3303 3288 3296 3236 3857 3292 3236 3857 7 320.0 297.68533 1 1 1 1 1 1 0.971 0.988 0.976 0.971 0.992 0.984 0 -33.9
11 12 6.050039 47.995344 2762 2736 2740 2747 3893 2736 2736 3893 5 390.0 368.55121 1 1 1 1 1 1 0.975 0.990 0.979 0.975 0.994 0.987 0 -37.3
14 15 6.050046 49.865317 1398 2505 2509 1316 2848 2505 1316 2848 6 340.0 330.40564 1 1 1 1 1 1 0.973 0.990 0.979 0.973 0.994 0.986 0 -18.2
15 16 6.050048 49.050020 984 943 947 958 2617 947 943 2617 6 300.0 291.22598 1 1 1 1 1 1 0.978 0.991 0.982 0.978 0.995 0.988 0 -35.4
16 17 6.050049 48.391359 3362 3332 3336 3351 4467 3336 3332 4467 5 530.0 504.78122 1 1 1 1 1 1 0.973 0.988 0.977 0.973 0.992 0.984 0 -5.1
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1267207 1267208 9.949829 49.216272 2160 2816 2816 2104 3299 2816 2104 3299 8 420.0 386.44556 1 1 1 1 1 1 0.980 0.993 0.984 0.980 0.995 0.989 0 -16.9
1267211 1267212 9.949856 49.881190 3190 3179 3179 3171 3822 3179 3171 3822 6 380.0 363.69348 1 1 1 1 1 1 0.968 0.986 0.974 0.968 0.990 0.982 0 -35.1
1267216 1267217 9.949880 49.873435 2061 2828 2046 2024 2828 2828 2024 2828 7 380.0 361.06812 1 1 1 1 1 1 0.967 0.988 0.974 0.967 0.993 0.983 0 -35.1
1267227 1267228 9.949958 49.127182 366 2307 1260 355 3531 2719 355 3531 6 500.0 493.52792 1 1 1 1 1 1 0.973 0.989 0.978 0.973 0.993 0.985 0 -36.0
1267237 1267238 9.949999 49.936763 2513 2490 2490 2494 2490 2490 2490 2513 5 360.0 346.54227 1 1 1 1 1 1 0.968 0.988 0.974 0.968 0.993 0.983 0 -32.2

226892 rows × 28 columns

Calculate the mean height excluidng the maximum and minimum values

[27]:

height_sel =  pd.DataFrame({'ID' : height_6algorithms_sel['ID'] ,
                            'hm_sel': (height_6algorithms_sel['a1_95'] + height_6algorithms_sel['a2_95'] + height_6algorithms_sel['a3_95'] + height_6algorithms_sel['a4_95']
                             + height_6algorithms_sel['a5_95'] + height_6algorithms_sel['a6_95'] - height_6algorithms_sel['min_rh_95'] - height_6algorithms_sel['max_rh_95']) / 400 } )

[28]:

height_sel

[28]:
ID hm_sel
7 8 32.9475
11 12 27.4625
14 15 22.2925
15 16 9.5900
16 17 33.4625
... ... ...
1267207 1267208 26.5200
1267211 1267212 31.8175
1267216 1267217 24.4075
1267227 1267228 16.6300
1267237 1267238 24.9100

226892 rows × 2 columns

Merge the new height with the predictors table, using the ID as Primary Key

[29]:

predictors_hm_sel = pd.merge( predictors ,  height_sel , left_on='ID' ,  right_on='ID' ,  how='right')

[30]:

predictors_hm_sel.head(6)

[30]:
ID X Y h BLDFIE_WeigAver CECSOL_WeigAver CHELSA_bio18 CHELSA_bio4 convergence cti devmagnitude eastness elev forestheight glad_ard_SVVI_max glad_ard_SVVI_med glad_ard_SVVI_min northness ORCDRC_WeigAver outlet_dist_dw_basin SBIO3_Isothermality_5_15cm SBIO4_Temperature_Seasonality_5_15cm treecover hm_sel
0 8 6.050019 49.921613 3294.75 1490 12 1995 5912 22.102139 -297770784 -1.402633 0.309765 294.927765 26 -86.729492 -145.584229 -190.062988 0.222435 15 772784 20.855963 457.195404 86 32.9475
1 12 6.050039 47.995344 2746.25 1523 12 2612 6181 3.549103 -71279992 0.507727 -0.021408 322.920227 26 660.006104 92.722168 190.979736 -0.034787 16 784807 20.798000 460.501221 97 27.4625
2 15 6.050046 49.865317 2229.25 1517 13 2191 5901 31.054762 -186807440 -1.375050 -0.126880 291.412537 7 1028.385498 915.806396 841.586182 0.024677 16 766444 19.941267 454.185089 54 22.2925
3 16 6.050048 49.050020 959.00 1526 14 2081 6100 9.933455 -183562672 -0.382834 0.086874 246.288010 24 -12.283691 -58.179199 174.205566 0.094175 10 805730 19.849365 470.946533 78 9.5900
4 17 6.050049 48.391359 3346.25 1489 19 2486 5966 -6.957157 -273522688 2.989759 0.214769 474.409088 24 125.583008 6.154297 128.129150 0.017164 15 950190 21.179420 491.398376 85 33.4625
5 19 6.050053 49.877876 529.00 1531 12 2184 5915 -24.278454 -377335296 0.265329 -0.248356 335.534760 25 593.601074 228.712402 315.298340 -0.127365 17 764713 19.760756 448.580811 96 5.2900 
[31]:

predictors_hm_sel = predictors_hm_sel.loc[(predictors['h'] < 7000) ].sample(100000)

[32]:

predictors_hm_sel

[32]:
ID X Y h BLDFIE_WeigAver CECSOL_WeigAver CHELSA_bio18 CHELSA_bio4 convergence cti devmagnitude eastness elev forestheight glad_ard_SVVI_max glad_ard_SVVI_med glad_ard_SVVI_min northness ORCDRC_WeigAver outlet_dist_dw_basin SBIO3_Isothermality_5_15cm SBIO4_Temperature_Seasonality_5_15cm treecover hm_sel
83357 447901 7.325923 49.296261 1988.00 1504 11 1973 6329 -27.310654 -311542144 1.611667 -0.059867 315.589905 22 99.902344 182.999268 358.212158 -0.027319 13 852606 18.866175 470.286011 75 19.8800
213105 1196478 9.622623 49.833063 2220.25 1520 13 1875 6606 -20.839262 -279513600 -0.550544 0.038211 244.721085 15 112.770508 -38.957520 -107.884766 -0.153021 11 770768 19.954826 507.755493 54 22.2025
58293 313301 7.017546 49.874260 1389.75 1525 14 2127 6080 -16.012159 -287215200 1.066931 -0.218266 424.159332 22 -59.042236 -32.115967 126.038086 0.068847 13 619919 19.761299 465.827271 85 13.8975
54985 297876 6.981116 48.889372 1883.25 1525 13 2161 6330 8.863924 431331168 -1.713272 0.013969 221.787323 23 560.937012 101.161133 27.694336 -0.025228 7 847969 18.343138 464.072418 67 18.8325
18698 98303 6.397619 49.380758 2965.00 1538 11 2367 6042 23.690971 -80957808 -0.130503 -0.035726 276.400085 25 230.774902 120.549805 309.234375 0.012809 13 740733 18.482462 444.627533 78 29.6500
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
60228 322853 7.040689 49.728151 3375.00 1402 12 2362 5810 17.660843 15303386 1.776377 0.010083 517.456360 25 172.217773 256.016113 213.990967 -0.079195 25 663180 21.064062 430.348450 85 33.7500
42226 231457 6.810772 48.268025 2707.00 1409 15 3120 6229 0.276158 -217058432 -0.143515 -0.099901 471.342743 25 -153.505615 -142.315430 -232.547607 -0.198644 29 955008 20.322662 441.391357 85 27.0700
49495 271346 6.916373 49.514878 3097.25 1536 13 2213 6140 -0.606761 -299815488 0.547743 -0.104366 365.085297 24 29.947266 -2.760986 204.209473 0.163875 14 789703 20.452227 469.161865 85 30.9725
11 40 6.050120 48.058094 3012.25 1521 14 2474 6191 -15.363133 -195105152 1.290480 -0.043498 331.926483 25 750.277832 12.481934 206.658447 -0.008241 15 820336 19.240412 474.946625 85 30.1225
185044 1039892 9.187669 49.500969 1117.00 1472 15 2561 6294 10.249912 -141432176 1.770781 -0.046596 483.281250 27 -15.297119 -161.964844 -210.821777 -0.015172 23 761513 19.522852 437.534729 38 11.1700

100000 rows × 24 columns

[33]:

   X = predictors_hm_sel.iloc[:,[4,5,6,7,8,9,10,11,12,14,15,16,17,18,19,20,21,22]].values
Y = predictors_hm_sel.iloc[:,23:24].values
feat = predictors_hm_sel.iloc[:,[4,5,6,7,8,9,10,11,12,14,15,16,17,18,19,20,21,22]].columns.values

[34]:

feat

[34]:

array(['BLDFIE_WeigAver', 'CECSOL_WeigAver', 'CHELSA_bio18',
       'CHELSA_bio4', 'convergence', 'cti', 'devmagnitude', 'eastness',
       'elev', 'glad_ard_SVVI_max', 'glad_ard_SVVI_med',
       'glad_ard_SVVI_min', 'northness', 'ORCDRC_WeigAver',
       'outlet_dist_dw_basin', 'SBIO3_Isothermality_5_15cm',
       'SBIO4_Temperature_Seasonality_5_15cm', 'treecover'], dtype=object)

[35]:

Y.shape

[35]:

(100000, 1)

[36]:

X.shape

[36]:

(100000, 18)

[37]:

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5, random_state=24)
y_train = np.ravel(Y_train)
y_test = np.ravel(Y_test)

Random Forest default parameters with select row base on quality flag

Training Random Forest using default parameters

[38]:

rfReg = RandomForestRegressor(min_samples_leaf=20, oob_score=True)
rfReg.fit(X_train, y_train);
dic_pred = {}
dic_pred['train'] = rfReg.predict(X_train)
dic_pred['test'] = rfReg.predict(X_test)

[39]:

# checking the oob score
rfReg.oob_score_

[39]:

0.37582774369799943

Final assesment

Selected data

[40]:

pearsonr_all_sel = [pearsonr(dic_pred['train'],y_train)[0],pearsonr(dic_pred['test'],y_test)[0]]
pearsonr_all_sel

[40]:

[0.747400101639897, 0.615726616845201]

All data

[41]:

pearsonr_all

[41]:

[0.6043347073198263, 0.5189400044676861]

Publication results

[42]:

pearsonr_Publication_Estimation

[42]:

0.4527925129990046

Tone the RF

pipeline = Pipeline([('rf',RandomForestRegressor())])

parameters = {
        'rf__max_features':("log2","sqrt",0.33),
        'rf__max_samples':(0.5,0.6,0.7),
        'rf__n_estimators':(500,1000),
        'rf__max_depth':(50,100,200)}

grid_search = GridSearchCV(pipeline,parameters,n_jobs=-1,cv=3,scoring='r2',verbose=1)
grid_search.fit(X_train,y_train)

grid_search.best_score_

print ('Best Training score: %0.3f' % grid_search.best_score_)
print ('Optimal parameters:')
best_par = grid_search.best_estimator_.get_params()
for par_name in sorted(parameters.keys()):
    print ('\t%s: %r' % (par_name, best_par[par_name]))

rfReg = RandomForestRegressor(n_estimators=500,max_features='sqrt',max_depth=50,max_samples=0.6,n_jobs=-1,random_state=24)
rfReg.fit(X_train, y_train);
dic_pred = {}
dic_pred['train'] = rfReg.predict(X_train)
dic_pred['test'] = rfReg.predict(X_test)
[pearsonr(dic_pred['train'],y_train)[0],pearsonr(dic_pred['test'],y_test)[0]]

[43]:

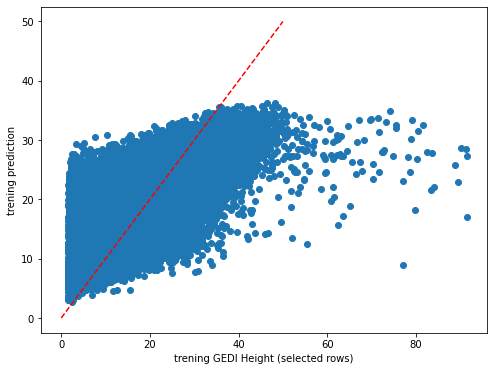
plt.rcParams["figure.figsize"] = (8,6)
plt.scatter(y_train,dic_pred['train'])
plt.xlabel('trening GEDI Height (selected rows)')
plt.ylabel('trening prediction')
ident = [0, 50]
plt.plot(ident,ident,'r--')

[43]:

[<matplotlib.lines.Line2D at 0x7fa0315145e0>]
../_images/CASESTUDY_Tree_Height_03RF_pred_74_1.png 
[44]:

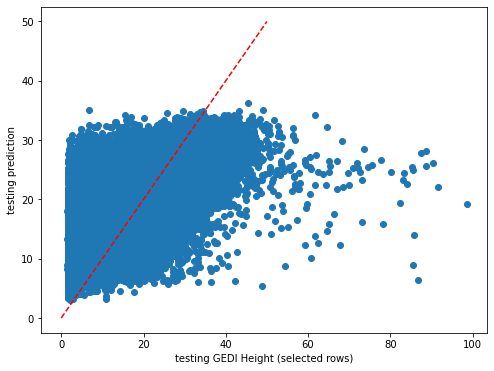
plt.rcParams["figure.figsize"] = (8,6)
plt.scatter(y_test,dic_pred['test'])
plt.xlabel('testing GEDI Height (selected rows)')
plt.ylabel('testing prediction')
ident = [0, 50]
plt.plot(ident,ident,'r--')

[44]:

[<matplotlib.lines.Line2D at 0x7fa0226b4d30>]
../_images/CASESTUDY_Tree_Height_03RF_pred_75_1.png 
[45]:

impt = [rfReg.feature_importances_, np.std([tree.feature_importances_ for tree in rfReg.estimators_],axis=1)]
ind = np.argsort(impt[0])

[46]:

ind

[46]:

array([ 1, 13,  0,  6, 16,  4,  8,  5,  3,  2, 15, 11, 12,  9, 14,  7, 10,
       17])

[47]:

plt.rcParams["figure.figsize"] = (6,12)
plt.barh(range(len(feat)),impt[0][ind],color="b", xerr=impt[1][ind], align="center")
plt.yticks(range(len(feat)),feat[ind]);
../_images/CASESTUDY_Tree_Height_03RF_pred_78_0.png

Predict on the raster using pyspatialml

[54]:

# import satalite indeces
glad_ard_SVVI_min = "tree_height/geodata_raster/glad_ard_SVVI_min.tif"
glad_ard_SVVI_med = "tree_height/geodata_raster/glad_ard_SVVI_med.tif"
glad_ard_SVVI_max = "tree_height/geodata_raster/glad_ard_SVVI_max.tif"

# import climate
CHELSA_bio4 = "tree_height/geodata_raster/CHELSA_bio4.tif"
CHELSA_bio18 = "tree_height/geodata_raster/CHELSA_bio18.tif"

# soil
BLDFIE_WeigAver = "tree_height/geodata_raster/BLDFIE_WeigAver.tif"
CECSOL_WeigAver = "tree_height/geodata_raster/CECSOL_WeigAver.tif"
ORCDRC_WeigAver = "tree_height/geodata_raster/ORCDRC_WeigAver.tif"

# Geomorphological
elev = "tree_height/geodata_raster/elev.tif"
convergence = "tree_height/geodata_raster/convergence.tif"
northness = "tree_height/geodata_raster/northness.tif"
eastness = "tree_height/geodata_raster/eastness.tif"
devmagnitude = "tree_height/geodata_raster/devmagnitude.tif"

# Hydrography
cti = "tree_height/geodata_raster/cti.tif"
outlet_dist_dw_basin = "tree_height/geodata_raster/outlet_dist_dw_basin.tif"

# Soil climate

SBIO3_Isothermality_5_15cm = "tree_height/geodata_raster/SBIO3_Isothermality_5_15cm.tif"
SBIO4_Temperature_Seasonality_5_15cm = "tree_height/geodata_raster/SBIO4_Temperature_Seasonality_5_15cm.tif"

# forest

treecover = "tree_height/geodata_raster/treecover.tif"

[56]:

treecover

[56]:

'tree_height/geodata_raster/treecover.tif'

[59]:

predictors_rasters = [glad_ard_SVVI_min, glad_ard_SVVI_med, glad_ard_SVVI_max,
                      CHELSA_bio4,CHELSA_bio18,
                      BLDFIE_WeigAver,CECSOL_WeigAver,ORCDRC_WeigAver,
                      elev,convergence,northness,eastness,devmagnitude,cti,outlet_dist_dw_basin,
                      SBIO3_Isothermality_5_15cm,SBIO4_Temperature_Seasonality_5_15cm,treecover]

stack = Raster(predictors_rasters)

[60]:

result = stack.predict(estimator=rfReg, dtype='int16', nodata=-1)

[53]:

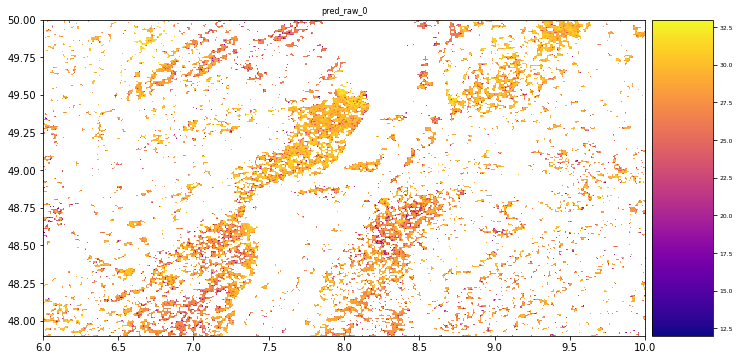
# plot regression result
plt.rcParams["figure.figsize"] = (12,12)
result.iloc[0].cmap = "plasma"
result.plot()
plt.show()
../_images/CASESTUDY_Tree_Height_03RF_pred_84_0.png